名称
ST_Contains — 测试B的每个点是否都位于A中,且它们的内部有共同点
概要
boolean ST_Contains(geometry geomA, geometry geomB);
描述
如果几何体A包含几何体B,则返回TRUE。当且仅当B的所有点都位于A的内部(即A的内部或边界)时(或者等效地,B的任何点都不位于A的外部),并且A和B的内部至少有一个共同点,则A包含B。
用数学术语表示:ST_Contains(A, B) ⇔ (A ⋂ B = B) ∧ (Int(A) ⋂ Int(B) ≠ ∅)
包含关系是自反的:每个几何体都包含自身。(相反,在ST_ContainsProperly谓词中,一个几何体不会恰当地包含自身。)该关系是反对称的:如果ST_Contains(A,B) = true 且 ST_Contains(B,A) = true,则两个几何体必须在拓扑上相等(ST_Equals(A,B) = true)。
ST_Contains 与 ST_Within 是互逆的。因此,ST_Contains(A,B) = ST_Within(B,A)。
![[Note]](../images/note.png)
|
|
|
由于内部必须有一个共同点,因此定义的微妙之处在于,多边形和线不包含完全位于其边界上的线和点。有关更多详细信息,请参见OGC Covers, Contains, Within 的微妙之处。ST_Covers 谓词提供了更具包容性的关系。 |
![[Note]](../images/note.png)
|
|
|
此函数自动包含边界框比较,该比较利用几何体上可用的任何空间索引。要避免使用索引,请使用函数 |
由 GEOS 模块执行
增强功能:2.3.0 PIP 短路增强扩展为支持具有少量点的 MultiPoint。早期版本仅支持多边形中的点。
![[Important]](../images/important.png)
|
|
|
增强功能:3.0.0 启用对 |
![[Important]](../images/important.png)
|
|
|
请勿将此函数与无效的几何体一起使用。您将获得意想不到的结果。 |
注意:这是返回布尔值而不是整数的“允许”版本。
 此方法实现了OGC 简单要素 SQL 1.1 实现规范。s2.1.1.2 // s2.1.13.3 - 与 within(geometry B, geometry A) 相同
此方法实现了OGC 简单要素 SQL 1.1 实现规范。s2.1.1.2 // s2.1.13.3 - 与 within(geometry B, geometry A) 相同
 此方法实现了 SQL/MM 规范。SQL-MM 3: 5.1.31
此方法实现了 SQL/MM 规范。SQL-MM 3: 5.1.31
示例
在以下情况下,ST_Contains 返回 TRUE

|
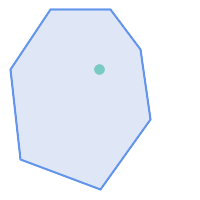
|
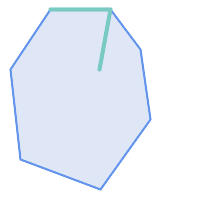
|
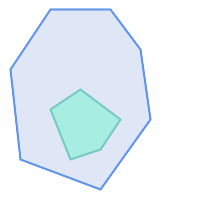
|
在以下情况下,ST_Contains 返回 FALSE
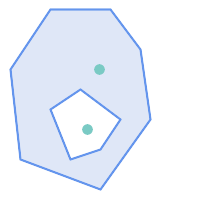
|
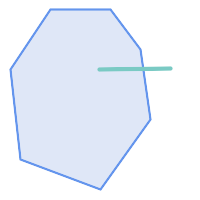
|
由于内部相交条件,在以下情况下 ST_Contains 返回 FALSE (而 ST_Covers 返回 TRUE)

|
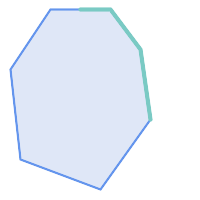
|
-- A circle within a circle
SELECT ST_Contains(smallc, bigc) As smallcontainsbig,
ST_Contains(bigc,smallc) As bigcontainssmall,
ST_Contains(bigc, ST_Union(smallc, bigc)) as bigcontainsunion,
ST_Equals(bigc, ST_Union(smallc, bigc)) as bigisunion,
ST_Covers(bigc, ST_ExteriorRing(bigc)) As bigcoversexterior,
ST_Contains(bigc, ST_ExteriorRing(bigc)) As bigcontainsexterior
FROM (SELECT ST_Buffer(ST_GeomFromText('POINT(1 2)'), 10) As smallc,
ST_Buffer(ST_GeomFromText('POINT(1 2)'), 20) As bigc) As foo;
-- Result
smallcontainsbig | bigcontainssmall | bigcontainsunion | bigisunion | bigcoversexterior | bigcontainsexterior
------------------+------------------+------------------+------------+-------------------+---------------------
f | t | t | t | t | f
-- Example demonstrating difference between contains and contains properly
SELECT ST_GeometryType(geomA) As geomtype, ST_Contains(geomA,geomA) AS acontainsa, ST_ContainsProperly(geomA, geomA) AS acontainspropa,
ST_Contains(geomA, ST_Boundary(geomA)) As acontainsba, ST_ContainsProperly(geomA, ST_Boundary(geomA)) As acontainspropba
FROM (VALUES ( ST_Buffer(ST_Point(1,1), 5,1) ),
( ST_MakeLine(ST_Point(1,1), ST_Point(-1,-1) ) ),
( ST_Point(1,1) )
) As foo(geomA);
geomtype | acontainsa | acontainspropa | acontainsba | acontainspropba
--------------+------------+----------------+-------------+-----------------
ST_Polygon | t | f | f | f
ST_LineString | t | f | f | f
ST_Point | t | t | f | f