描述

返回一组几何图形，这些几何图形是通过使用直线将 geom 分成多个部分而得到的，每个部分包含不超过 max_vertices 个顶点。

max_vertices 必须大于或等于 5，因为表示一个封闭的框需要 5 个点。可以指定 gridSize 使得裁剪在固定精度空间中工作（需要 GEOS-3.9.0+）。

点在多边形内以及其他空间操作通常对于索引细分数据集来说更快。由于各个部分的边界框通常比原始几何图形的边界框覆盖的面积更小，因此索引查询会产生更少的“命中”情况。“命中”情况更快，因为索引重新检查过程执行的空间操作检查的点更少。

	这是一个 返回集合的函数 (SRF)，它返回一组包含单个几何图形值的记录。它可以在 SELECT 列表或 FROM 子句中使用，以生成一个结果集，其中每个结果几何图形对应一个记录。

由 GEOS 模块执行。

可用性：2.2.0

增强：2.5.0 重用多边形分割时已有的点，顶点数从 8 降至 5。

增强：3.1.0 接受 gridSize 参数。

需要 GEOS >= 3.9.0 才能使用 gridSize 参数

示例

示例： 将一个多边形细分成顶点数不超过 10 个的部分，并为每个部分分配一个唯一的 ID。

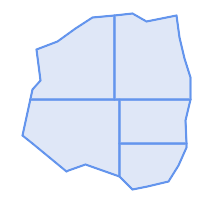
细分为最多 10 个顶点

SELECT row_number() OVER() As rn, ST_AsText(geom) As wkt
    FROM (SELECT ST_SubDivide(
        'POLYGON((132 10,119 23,85 35,68 29,66 28,49 42,32 56,22 64,32 110,40 119,36 150,
        57 158,75 171,92 182,114 184,132 186,146 178,176 184,179 162,184 141,190 122,
        190 100,185 79,186 56,186 52,178 34,168 18,147 13,132 10))'::geometry,10))  AS f(geom);

 rn │                                                      wkt
────┼────────────────────────────────────────────────────────────────────────────────────────────────────────────────
  1 │ POLYGON((119 23,85 35,68 29,66 28,32 56,22 64,29.8260869565217 100,119 100,119 23))
  2 │ POLYGON((132 10,119 23,119 56,186 56,186 52,178 34,168 18,147 13,132 10))
  3 │ POLYGON((119 56,119 100,190 100,185 79,186 56,119 56))
  4 │ POLYGON((29.8260869565217 100,32 110,40 119,36 150,57 158,75 171,92 182,114 184,114 100,29.8260869565217 100))
  5 │ POLYGON((114 184,132 186,146 178,176 184,179 162,184 141,190 122,190 100,114 100,114 184))
  

示例： 使用 ST_Segmentize(geography, distance) 对一条很长的地理线进行加密，并使用 ST_Subdivide 将生成的线细分成 8 个顶点的子线。

加密和细分的线。

SELECT ST_AsText( ST_Subdivide(
            ST_Segmentize('LINESTRING(0 0, 85 85)'::geography,
                          1200000)::geometry,    8));

LINESTRING(0 0,0.487578359029357 5.57659056746196,0.984542144675897 11.1527721155093,1.50101059639722 16.7281035483571,1.94532113630331 21.25)
LINESTRING(1.94532113630331 21.25,2.04869538062779 22.3020741387339,2.64204641967673 27.8740533545155,3.29994062412787 33.443216802941,4.04836719489742 39.0084282520239,4.59890468420694 42.5)
LINESTRING(4.59890468420694 42.5,4.92498503922732 44.5680389206321,5.98737409390639 50.1195229244701,7.3290919767674 55.6587646879025,8.79638749938413 60.1969505994924)
LINESTRING(8.79638749938413 60.1969505994924,9.11375579533779 61.1785363177625,11.6558166691368 66.6648504160202,15.642041247655 72.0867690601745,22.8716627200212 77.3609628116894,24.6991785131552 77.8939011989848)
LINESTRING(24.6991785131552 77.8939011989848,39.4046096622744 82.1822848017636,44.7994523421035 82.5156766227011)
LINESTRING(44.7994523421035 82.5156766227011,85 85)

示例： 对表中的复杂几何图形进行就地细分。原始几何图形记录从源表中删除，并为每个细分结果几何图形插入新的记录。

WITH complex_areas_to_subdivide AS (
    DELETE from polygons_table
    WHERE ST_NPoints(geom) > 255
    RETURNING id, column1, column2, column3, geom
)
INSERT INTO polygons_table (fid, column1, column2, column3, geom)
    SELECT fid, column1, column2, column3,
           ST_Subdivide(geom, 255) as geom
    FROM complex_areas_to_subdivide;

示例： 创建一个包含细分几何图形的新表，保留原始几何图形的键，以便新表可以与源表进行联接。由于 ST_Subdivide 是一个返回集合的（表）函数，它返回一组单值行，因此此语法会自动生成一个表，其中每个结果部分对应一行。

CREATE TABLE subdivided_geoms AS
    SELECT pkey, ST_Subdivide(geom) AS geom
    FROM original_geoms;

另请参阅

ST_ClipByBox2D、ST_Segmentize、ST_Split、ST_NPoints