名称
CG_MinkowskiSum — 执行闵可夫斯基和
概要
geometry CG_MinkowskiSum(geometry geom1, geometry geom2);
描述
此函数执行点、线或多边形与多边形的 2D 闵可夫斯基和。
两个几何体 A 和 B 的闵可夫斯基和是 A 和 B 中任意点的和的所有点的集合。闵可夫斯基和常用于运动规划和计算机辅助设计。更多详细信息请参阅 维基百科闵可夫斯基加法。
第一个参数可以是任何 2D 几何体(点、线串、多边形)。如果传递 3D 几何体,它将通过强制 Z 为 0 转换为 2D,从而可能导致无效的情况。第二个参数必须是 2D 多边形。
实现利用了 CGAL 2D 闵可夫斯基和。
可用性:3.5.0
 此方法需要 SFCGAL 后端。
此方法需要 SFCGAL 后端。
示例
线串和圆多边形的闵可夫斯基和,其中线串穿过圆
|
 求和前
|
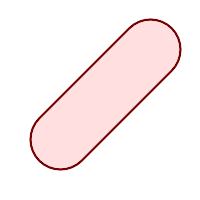 求和后
|
SELECT CG_MinkowskiSum(line, circle))
FROM (SELECT
ST_MakeLine(ST_Point(10, 10),ST_Point(100, 100)) As line,
ST_Buffer(ST_GeomFromText('POINT(50 50)'), 30) As circle) As foo;
-- wkt --
MULTIPOLYGON(((30 59.9999999999999,30.5764415879031 54.1472903395161,32.2836140246614 48.5194970290472,35.0559116309237 43.3328930094119,38.7867965644036 38.7867965644035,43.332893009412 35.0559116309236,48.5194970290474 32.2836140246614,54.1472903395162 30.5764415879031,60.0000000000001 30,65.8527096604839 30.5764415879031,71.4805029709527 32.2836140246614,76.6671069905881 35.0559116309237,81.2132034355964 38.7867965644036,171.213203435596 128.786796564404,174.944088369076 133.332893009412,177.716385975339 138.519497029047,179.423558412097 144.147290339516,180 150,179.423558412097 155.852709660484,177.716385975339 161.480502970953,174.944088369076 166.667106990588,171.213203435596 171.213203435596,166.667106990588 174.944088369076,
161.480502970953 177.716385975339,155.852709660484 179.423558412097,150 180,144.147290339516 179.423558412097,138.519497029047 177.716385975339,133.332893009412 174.944088369076,128.786796564403 171.213203435596,38.7867965644035 81.2132034355963,35.0559116309236 76.667106990588,32.2836140246614 71.4805029709526,30.5764415879031 65.8527096604838,30 59.9999999999999)))
多边形和多点的闵可夫斯基和
|
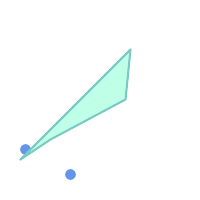 求和前
|
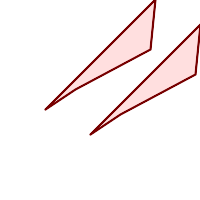 求和后:多边形被复制并平移到点的位置
|
SELECT CG_MinkowskiSum(mp, poly)
FROM (SELECT 'MULTIPOINT(25 50,70 25)'::geometry As mp,
'POLYGON((130 150, 20 40, 50 60, 125 100, 130 150))'::geometry As poly
) As foo
-- wkt --
MULTIPOLYGON(
((70 115,100 135,175 175,225 225,70 115)),
((120 65,150 85,225 125,275 175,120 65))
)