24. 等值

24.1. 等值

在处理几何图形时，确定等值可能很棘手。PostGIS 支持三种不同的函数，可用于确定不同级别的等值，但为了清晰起见，我们将使用以下定义。为了说明这些函数，我们将使用以下多边形。

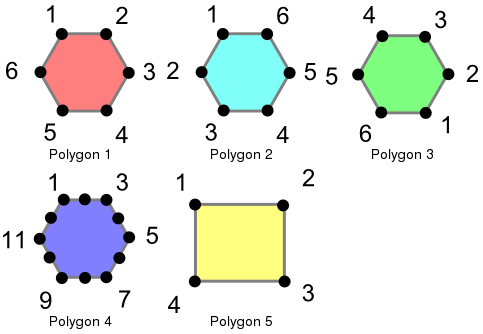
_images/polygon-table.png

这些多边形使用以下命令加载。

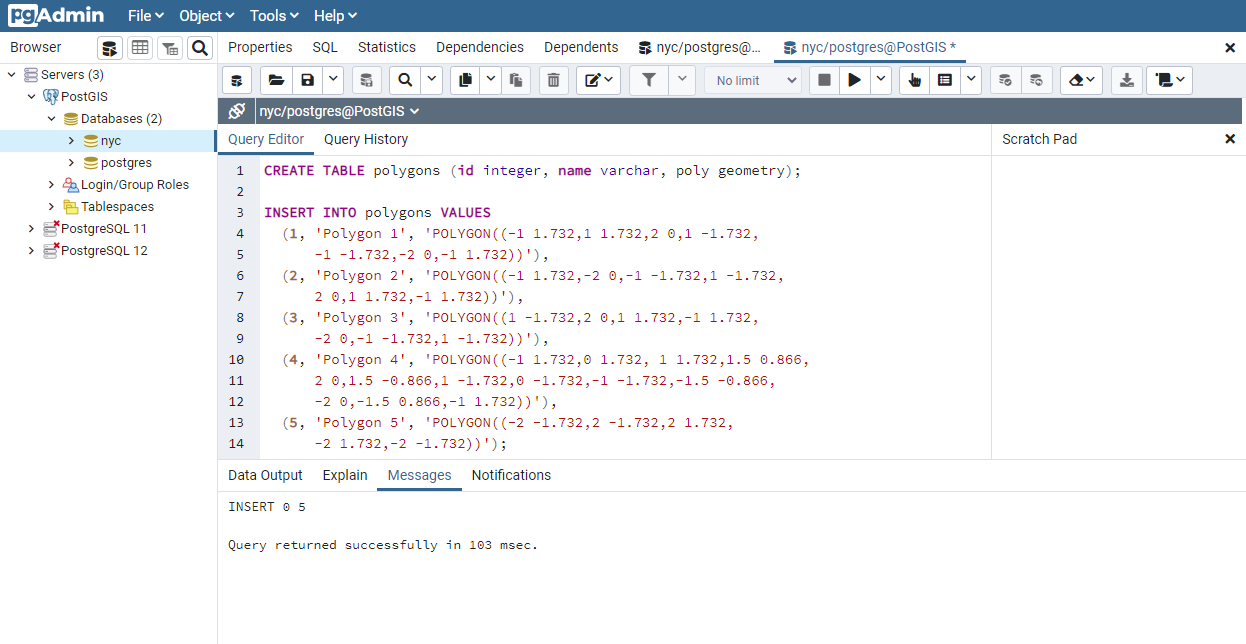
CREATE TABLE polygons (id integer, name varchar, poly geometry);

INSERT INTO polygons VALUES
  (1, 'Polygon 1', 'POLYGON((-1 1.732,1 1.732,2 0,1 -1.732,
      -1 -1.732,-2 0,-1 1.732))'),
  (2, 'Polygon 2', 'POLYGON((-1 1.732,-2 0,-1 -1.732,1 -1.732,
      2 0,1 1.732,-1 1.732))'),
  (3, 'Polygon 3', 'POLYGON((1 -1.732,2 0,1 1.732,-1 1.732,
      -2 0,-1 -1.732,1 -1.732))'),
  (4, 'Polygon 4', 'POLYGON((-1 1.732,0 1.732, 1 1.732,1.5 0.866,
      2 0,1.5 -0.866,1 -1.732,0 -1.732,-1 -1.732,-1.5 -0.866,
      -2 0,-1.5 0.866,-1 1.732))'),
  (5, 'Polygon 5', 'POLYGON((-2 -1.732,2 -1.732,2 1.732,
      -2 1.732,-2 -1.732))');
_images/start13.png

24.1.1. 完全相等

完全相等是通过逐个顶点比较两个几何图形来确定的，以确保它们在位置上完全相同。以下示例显示了这种方法在有效性方面的局限性。

SELECT a.name, b.name,
  CASE WHEN ST_OrderingEquals(a.poly, b.poly)
       THEN 'Exactly Equal'
       ELSE 'Not Exactly Equal' END
  FROM polygons AS a, polygons AS b;
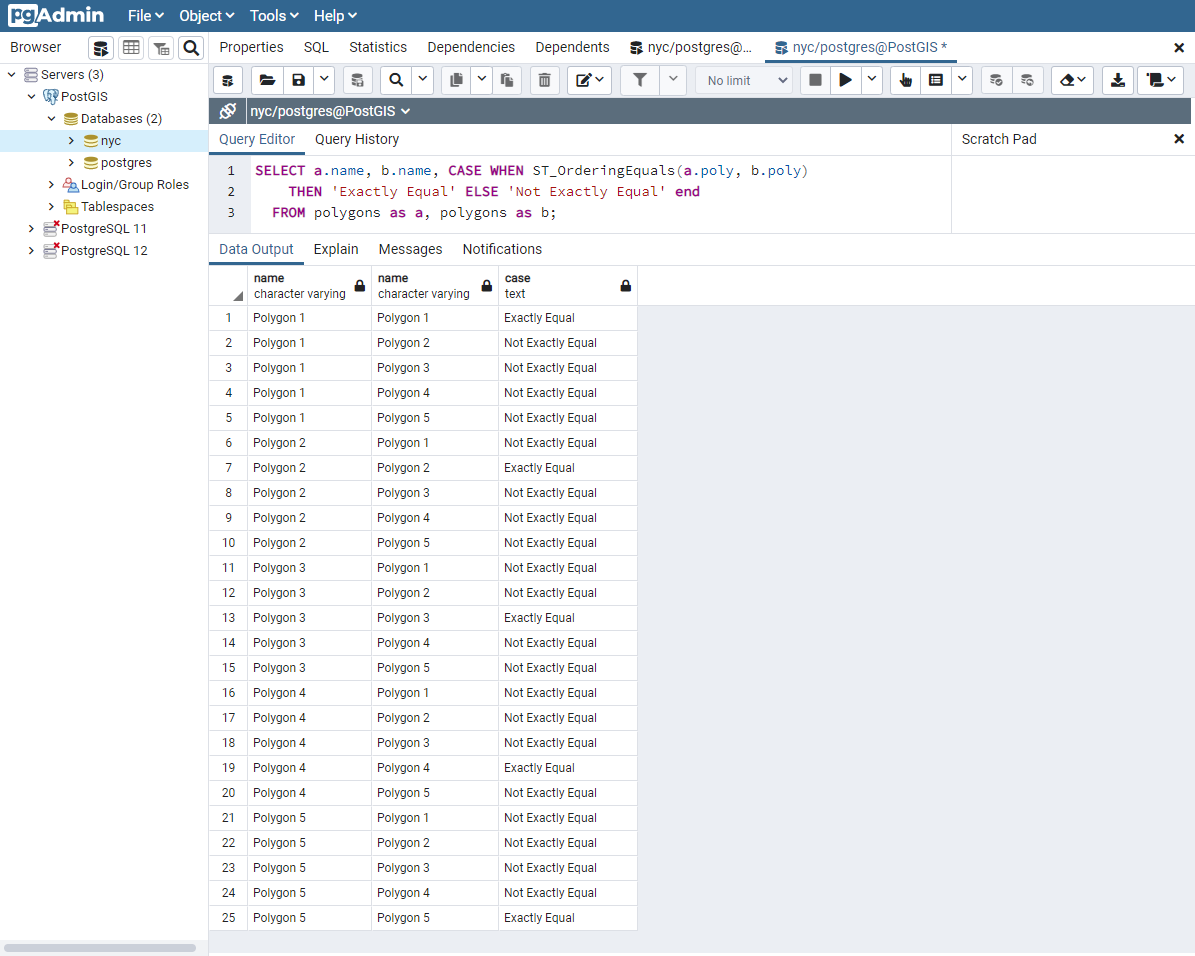
_images/start14.png

在此示例中，多边形仅与其自身相等，而不与其他看似等效的多边形相等（如多边形 1 到 3 的情况）。在多边形 1、2 和 3 的情况下，顶点位于相同的位置，但定义顺序不同。多边形 4 在六边形边上具有共线（因此是冗余的）顶点，导致与多边形 1 不相等。

24.1.2. 空间相等

如上所述，完全相等没有考虑几何图形的空间性质。有一个名为 ST_Equals 的函数，可用于测试几何图形的空间相等性或等效性。

SELECT a.name, b.name,
  CASE WHEN ST_Equals(a.poly, b.poly)
       THEN 'Spatially Equal'
       ELSE 'Not Equal' END
  FROM polygons AS a, polygons AS b;
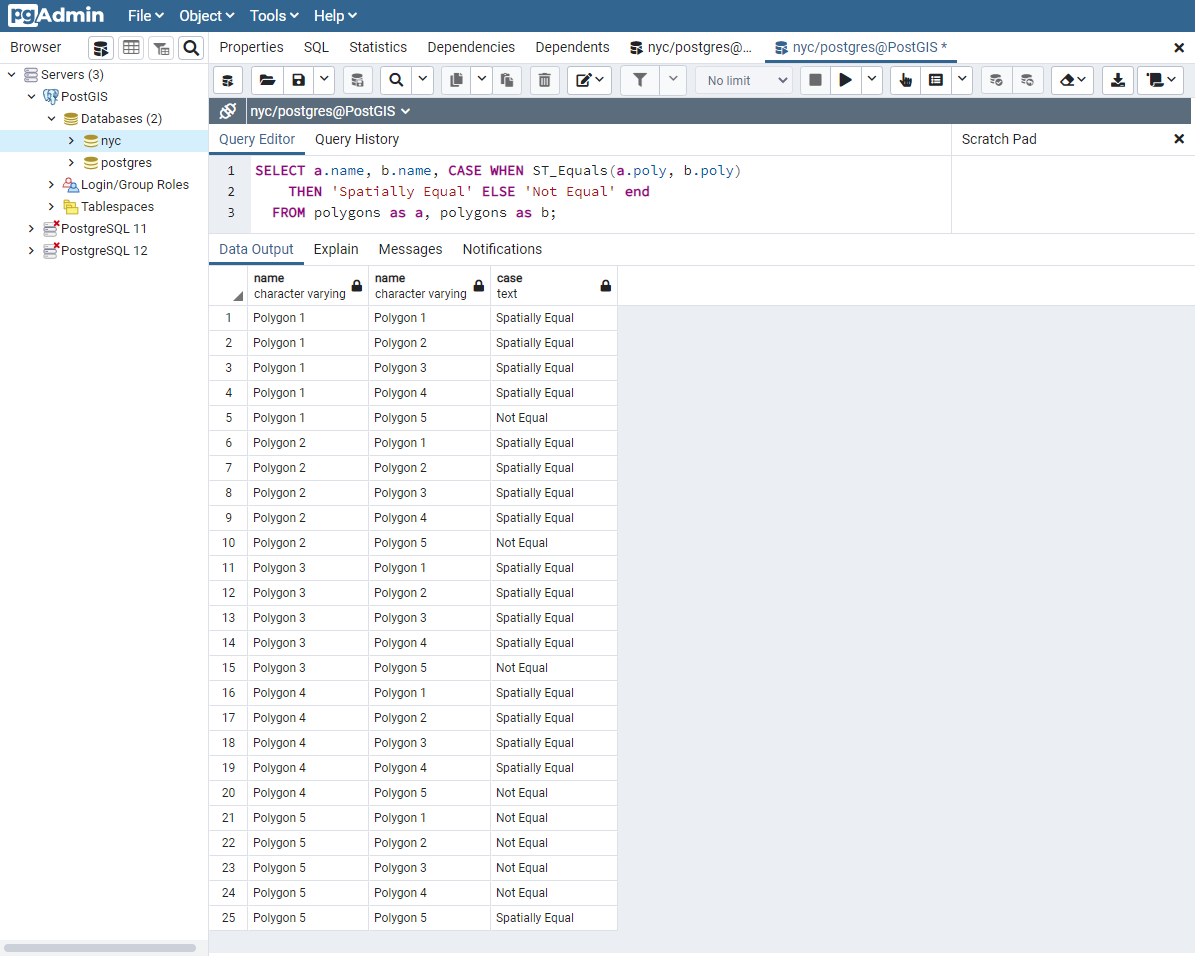
_images/start15.png

这些结果更符合我们对等值的直观理解。多边形 1 到 4 被认为是相等的，因为它们包含相同的区域。请注意，这里多边形的绘制方向、定义多边形的起点以及使用的点数都不重要。重要的是多边形包含相同的空间。

24.1.3. 边界相等

精确相等要求在最坏情况下比较几何体中的每个顶点以确定相等性。这可能很慢，并且可能不适合比较大量的几何体。为了允许更快的比较，提供了相等边界运算符 ~=。这仅对边界框（矩形）起作用，确保几何体占据相同的二维范围，但不一定占据相同的空间。

SELECT a.name, b.name,
  CASE WHEN a.poly ~= b.poly
       THEN 'Equal Bounds'
       ELSE 'Non-equal Bounds' END
  FROM polygons AS a, polygons AS b;
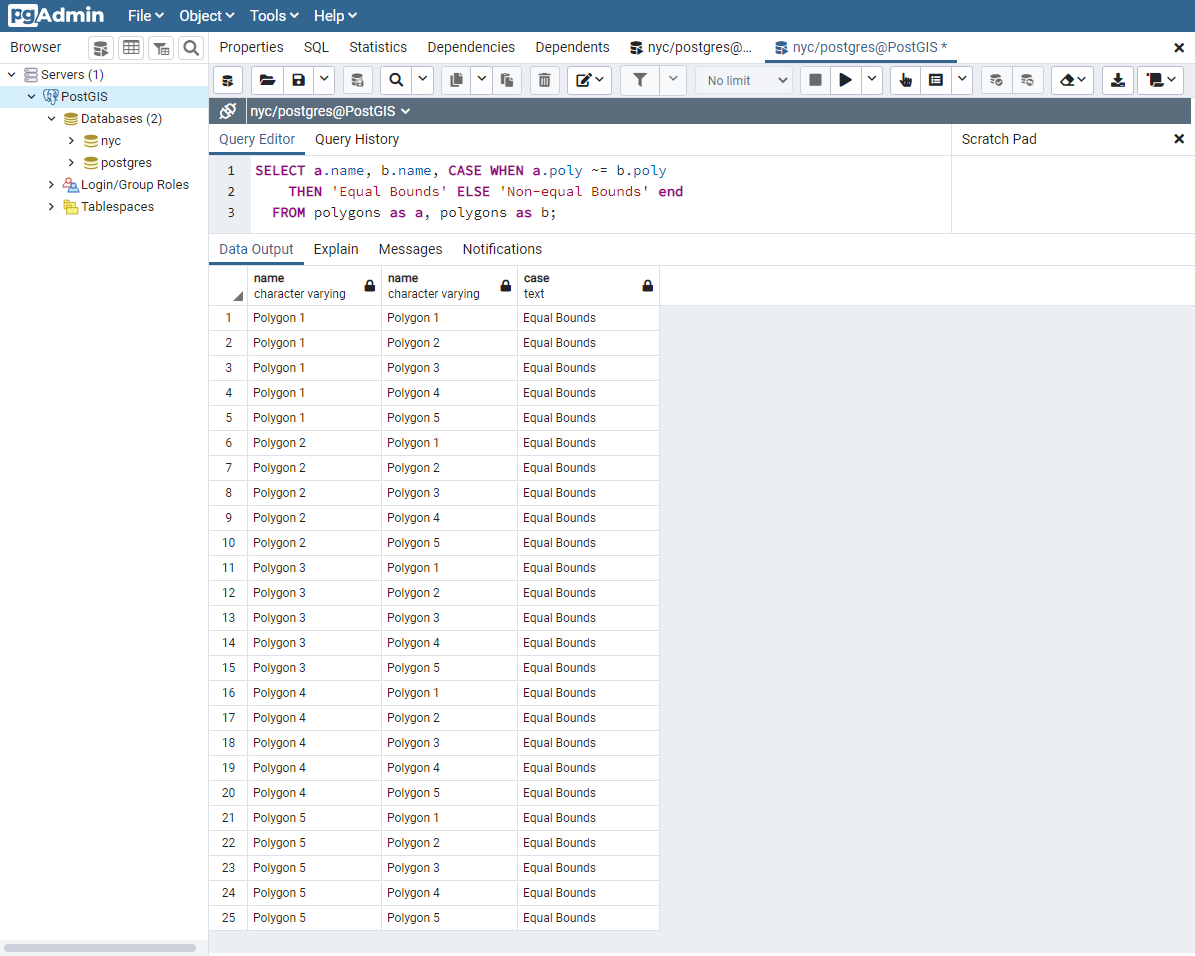
_images/start17.png

如您所见，我们所有空间相等的几何体也具有相等的边界。不幸的是，多边形 5 在此测试下也被返回为相等，因为它与其他几何体共享相同的边界框。那么，这有什么用呢？虽然这将在后面详细介绍，但简而言之，这使得可以使用空间索引，空间索引可以在连接或过滤数据时快速将巨大的比较集缩减为更易于管理的块。