第 5 章。空间查询
空间数据库的 存在理由 是在数据库内部执行通常需要桌面 GIS 功能的查询。有效使用 PostGIS 需要了解可用的空间函数,如何在查询中使用它们,并确保已设置适当的索引以提供良好的性能。
5.1. 确定空间关系
空间关系表示两个几何图形如何相互作用。它们是查询几何图形的基本能力。
5.1.1. 维度扩展的 9 交集模型
根据 OpenGIS 简单要素 SQL 实现规范,“比较两个几何图形的基本方法是对两个几何图形的内部、边界和外部之间的交集进行成对测试,并根据结果的“交集”矩阵中的条目对两个几何图形之间的关系进行分类。”
在点集拓扑理论中,嵌入在二维空间中的几何图形中的点分为三组
- 边界
-
几何图形的边界是下一维度的几何图形的集合。对于维度为 0 的
POINT,边界是空集。LINESTRING的边界是两个端点。对于POLYGON,边界是外部和内部环的线段。 - 内部
-
几何图形的内部是几何图形中不在边界上的点。对于
POINT,内部是点本身。LINESTRING的内部是端点之间的一组点。对于POLYGON,内部是多边形内的面积。 - 外部
-
几何图形的外部是几何图形嵌入的空间的其余部分;换句话说,是不在几何图形内部或边界上的所有点。它是一个二维非封闭表面。
维度扩展的 9 交集模型 (DE-9IM) 通过指定每个几何图形的上述集合之间的 9 个交集的维度来描述两个几何图形之间的空间关系。交集维度可以用 3x3 交集矩阵 正式表示。
对于几何图形 g,内部、边界 和 外部 使用符号 I(g)、B(g) 和 E(g) 表示。此外,dim(s) 表示集合 s 的维度,其域为 {0,1,2,F}
-
0=> 点 -
1=> 线 -
2=> 区域 -
F=> 空集
使用此符号,两个几何图形 a 和 b 的交集矩阵为
| 内部 | 边界 | 外部 | |
|---|---|---|---|
| 内部 | dim( I(a) ∩ I(b) ) | dim( I(a) ∩ B(b) ) | dim( I(a) ∩ E(b) ) |
| 边界 | dim( B(a) ∩ I(b) ) | dim( B(a) ∩ B(b) ) | dim( B(a) ∩ E(b) ) |
| 外部 | dim( E(a) ∩ I(b) ) | dim( E(a) ∩ B(b) ) | dim( E(a) ∩ E(b) ) |
在视觉上,对于两个重叠的多边形几何图形,它看起来像
|
||||||||||||||||||
|
|
从左到右和从上到下读取,交集矩阵表示为文本字符串“212101212”。
有关更多信息,请参阅
-
OpenGIS 简单要素 SQL 实现规范(1.1 版,第 2.1.13.2 节)
5.1.2. 命名的空间关系
为了方便确定常见的空间关系,OGC SFS 定义了一组命名的空间关系谓词。PostGIS 将这些作为函数 ST_Contains、ST_Crosses、ST_Disjoint、ST_Equals、ST_Intersects、ST_Overlaps、ST_Touches、ST_Within 提供。它还定义了非标准关系谓词 ST_Covers、ST_CoveredBy 和 ST_ContainsProperly。
空间谓词通常用作 SQL WHERE 或 JOIN 子句中的条件。命名的空间谓词会自动使用空间索引(如果可用),因此无需同时使用边界框运算符 &&。例如
SELECT city.name, state.name, city.geom FROM city JOIN state ON ST_Intersects(city.geom, state.geom);
有关更多详细信息和示例,请参阅 PostGIS Workshop。
5.1.3. 一般空间关系
在某些情况下,命名的空间关系不足以提供所需的空间过滤器条件。
 例如,考虑一个表示道路网络的线性数据集。可能需要识别彼此交叉的所有路段,而不是在某个点上,而是在一条线上(可能是为了验证某些业务规则)。在这种情况下,ST_Crosses 不提供必要的空间过滤器,因为对于线性要素,它仅在其在某一点交叉时才返回 一个两步解决方案是首先计算空间上相交 (ST_Intersects) 的成对道路线的实际交集 (ST_Intersection),然后检查交集的 ST_GeometryType 是否为“ 显然,需要一种更简单、更快速的解决方案。 |
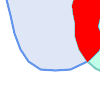
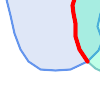
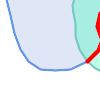
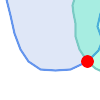
 第二个示例是定位在一条线上与湖泊边界相交的码头,并且码头的一端位于岸上。换句话说,码头在湖泊内但不完全被湖泊包含,在一条线上与湖泊的边界相交,并且码头的端点之一在湖泊的边界内或边界上。可以使用空间谓词的组合来查找所需的要素
|
这些要求可以通过计算完整的 DE-9IM 交集矩阵来满足。PostGIS 提供了 ST_Relate 函数来执行此操作
SELECT ST_Relate( 'LINESTRING (1 1, 5 5)',
'POLYGON ((3 3, 3 7, 7 7, 7 3, 3 3))' );
st_relate
-----------
1010F0212
要测试特定的空间关系,请使用交集矩阵模式。这是用附加符号 {T,*} 扩充的矩阵表示
-
T=> 交集维度为非空;即在{0,1,2}中 -
*=> 不关心
使用交集矩阵模式,可以以更简洁的方式评估特定的空间关系。ST_Relate 和 ST_RelateMatch 函数可用于测试交集矩阵模式。对于上面的第一个示例,指定两条线在线中相交的交集矩阵模式是“1*1***1**”
-- Find road segments that intersect in a line
SELECT a.id
FROM roads a, roads b
WHERE a.id != b.id
AND a.geom && b.geom
AND ST_Relate(a.geom, b.geom, '1*1***1**');
对于第二个示例,指定部分在多边形内部和部分在多边形外部的线的交集矩阵模式是“102101FF2”
-- Find wharves partly on a lake's shoreline
SELECT a.lake_id, b.wharf_id
FROM lakes a, wharfs b
WHERE a.geom && b.geom
AND ST_Relate(a.geom, b.geom, '102101FF2');
5.2. 使用空间索引
在使用空间条件构造查询时,为了获得最佳性能,务必确保使用空间索引(如果存在)(请参阅第 4.9 节,“空间索引”)。为此,必须在查询的 WHERE 或 ON 子句中使用空间运算符或索引感知函数。
空间运算符包括边界框运算符(其中最常用的是 &&;有关完整列表,请参阅第 7.10.1 节,“边界框运算符”)和最近邻查询中使用的距离运算符(最常见的是 <->;有关完整列表,请参阅第 7.10.2 节,“距离运算符”)。
索引感知函数会自动将边界框运算符添加到空间条件。索引感知函数包括命名的空间关系谓词 ST_Contains、ST_ContainsProperly、ST_CoveredBy、ST_Covers、ST_Crosses、ST_Intersects、ST_Overlaps、ST_Touches、ST_Within、ST_Within 和 ST_3DIntersects,以及距离谓词 ST_DWithin、ST_DFullyWithin、ST_3DDFullyWithin 和 ST_3DDWithin。)
诸如 ST_Distance 之类的函数不使用索引来优化其操作。例如,以下查询在大型表上会非常慢
SELECT geom FROM geom_table WHERE ST_Distance( geom, 'SRID=312;POINT(100000 200000)' ) < 100
此查询选择 geom_table 中所有距离点 (100000, 200000) 在 100 个单位内的几何图形。这个查询会很慢,因为它需要计算表中每个点与指定点之间的距离,即对表中的每一行都计算一次 ST_Distance()。
使用支持索引的函数 ST_DWithin 可以大幅减少处理的行数。
SELECT geom FROM geom_table WHERE ST_DWithin( geom, 'SRID=312;POINT(100000 200000)', 100 )
此查询选择相同的几何图形,但以更高效的方式进行。这是通过 ST_DWithin() 在内部使用 && 运算符对查询几何图形的扩展边界框进行操作来实现的。如果 geom 上存在空间索引,查询计划器将识别出它可以利用索引来减少计算距离之前扫描的行数。空间索引允许仅检索几何图形边界框与扩展范围重叠的记录,因此这些记录可能在所需的距离内。然后计算实际距离以确认是否将该记录包含在结果集中。
有关更多信息和示例,请参阅 PostGIS Workshop。
5.3. 空间 SQL 示例
本节中的示例使用线性道路表和多边形市政边界表。bc_roads 表的定义是
Column | Type | Description ----------+-------------------+------------------- gid | integer | Unique ID name | character varying | Road Name geom | geometry | Location Geometry (Linestring)
bc_municipality 表的定义是
Column | Type | Description ---------+-------------------+------------------- gid | integer | Unique ID code | integer | Unique ID name | character varying | City / Town Name geom | geometry | Location Geometry (Polygon)
- 5.3.1. 所有道路的总长度(以公里为单位)是多少?
- 5.3.2. 乔治王子城的面积有多大(以公顷为单位)?
- 5.3.3. 该省面积最大的城市是哪个?
- 5.3.4. 完全包含在每个城市内的道路长度是多少?
- 5.3.5. 创建一个新表,其中包含乔治王子城内的所有道路。
- 5.3.6. 维多利亚的“Douglas St”的长度是多少(以公里为单位)?
- 5.3.7. 哪个是具有孔洞的最大市政多边形?
|
5.3.1. |
所有道路的总长度(以公里为单位)是多少? |
|
您可以使用一段非常简单的 SQL 来回答这个问题 SELECT sum(ST_Length(geom))/1000 AS km_roads FROM bc_roads; km_roads ------------------ 70842.1243039643 |
|
|
5.3.2. |
乔治王子城的面积有多大(以公顷为单位)? |
|
此查询将属性条件(在城市名称上)与空间计算(多边形面积)相结合 SELECT ST_Area(geom)/10000 AS hectares FROM bc_municipality WHERE name = 'PRINCE GEORGE'; hectares ------------------ 32657.9103824927 |
|
|
5.3.3. |
该省面积最大的城市是哪个? |
|
此查询使用空间测量值作为排序值。有几种方法可以解决这个问题,但最有效的方法如下 SELECT name, ST_Area(geom)/10000 AS hectares FROM bc_municipality ORDER BY hectares DESC LIMIT 1; name | hectares ---------------+----------------- TUMBLER RIDGE | 155020.02556131 请注意,为了回答此查询,我们必须计算每个多边形的面积。如果我们经常这样做,则向表中添加一个面积列以便为性能建立索引是有意义的。通过以降序排列结果,然后使用 PostgreSQL 的“LIMIT”命令,我们可以轻松地选择最大值,而无需使用 MAX() 之类的聚合函数。 |
|
|
5.3.4. |
完全包含在每个城市内的道路长度是多少? |
|
这是一个“空间连接”的示例,它将来自两个表的数据(使用连接)通过空间交互(“包含”)作为连接条件(而不是通常的在公共键上连接的关系方法)结合在一起 SELECT m.name, sum(ST_Length(r.geom))/1000 as roads_km FROM bc_roads AS r JOIN bc_municipality AS m ON ST_Contains(m.geom, r.geom) GROUP BY m.name ORDER BY roads_km; name | roads_km ----------------------------+------------------ SURREY | 1539.47553551242 VANCOUVER | 1450.33093486576 LANGLEY DISTRICT | 833.793392535662 BURNABY | 773.769091404338 PRINCE GEORGE | 694.37554369147 ... 这个查询需要一段时间,因为表中每条道路都被汇总到最终结果中(例如表约 25 万条道路)。对于较小的数据集(几千条记录和几百条记录),响应可能非常快。 |
|
|
5.3.5. |
创建一个新表,其中包含乔治王子城内的所有道路。 |
|
这是一个“叠加”的示例,它接收两个表,并输出一个新表,该表包含空间裁剪或切割的结果。与上面演示的“空间连接”不同,此查询创建了新的几何图形。叠加就像一个涡轮增压的空间连接,对于更精确的分析工作很有用 CREATE TABLE pg_roads as SELECT ST_Intersection(r.geom, m.geom) AS intersection_geom, ST_Length(r.geom) AS rd_orig_length, r.* FROM bc_roads AS r JOIN bc_municipality AS m ON ST_Intersects(r.geom, m.geom) WHERE m.name = 'PRINCE GEORGE'; |
|
|
5.3.6. |
维多利亚的“Douglas St”的长度是多少(以公里为单位)? |
SELECT sum(ST_Length(r.geom))/1000 AS kilometers FROM bc_roads r JOIN bc_municipality m ON ST_Intersects(m.geom, r.geom WHERE r.name = 'Douglas St' AND m.name = 'VICTORIA'; kilometers ------------------ 4.89151904172838 |
|
|
5.3.7. |
哪个是具有孔洞的最大市政多边形? |
SELECT gid, name, ST_Area(geom) AS area FROM bc_municipality WHERE ST_NRings(geom) > 1 ORDER BY area DESC LIMIT 1; gid | name | area -----+--------------+------------------ 12 | SPALLUMCHEEN | 257374619.430216 |